The problem here is to discover how to exactly foreshorten the whole 3 dimensional space, not just a 2 dimensional plane. That is, how to relate the foreshortening of the floor plane with the simultaneous foreshortening of the two vertical planes.

In 1990 several geometric formulae came to my mind that established the relationships between the exact foreshortening of the floor plane and the simultaneous exact foreshortening of the two vertical planes. "Exact" means: you can basically produce an image in linear perspective that in foreshortening is the same as a photograph taken of the same scene from the same standpoint from which the image is drawn.

To be able to draw 3 dimensional foreshortened volume in linear perspective, first imagine the space as a 3 dimensional Cartesian coordinate, i.e. as filled up with cubes of equal size of, say, 1 meter x 1 meter x 1 meter (which are then the coordinate points of the coordinate; see Figure 1).

Second, imagine where you stand. The formulae I’ve devised are derived from 2 different positions of your stance.

Perspective drawing can be said to be the translation of the 3 dimensional volume onto the 2 dimensional plane done from the translator's particular stance. Hence what we are doing is translating the 3 dimensional space seen by the artist in Figure 1 into a 2 dimensional screen.

Formula 1.A:

In this one the location you stand in is on a straight line drawn between the intersection of the two vertical planes of space (plane yz and plane yx) and you and which forms a 45 degree angle with either of the two vertical planes.

Figure 1: the artist's stand point for Formula 1.A.

In this one, furthermore, the lines of the vertical planes (in the y direction) do not eventually converge on a vanishing point (above or below the horizon line) but are perfectly parallel with one another. In other words, there is no foreshortening with regard to the height in this formula for the 3D linear perspective.

The diagonals (marked in red) – the determinant for the proportion of the foreshortening of a plane divided up into squares of equal size (the coordinates) – for the floor plane (plane xz) in this case should converge on a vanishing point that lies right in the middle of the horizon line, dividing it in half (Figure 2).

Figure 2

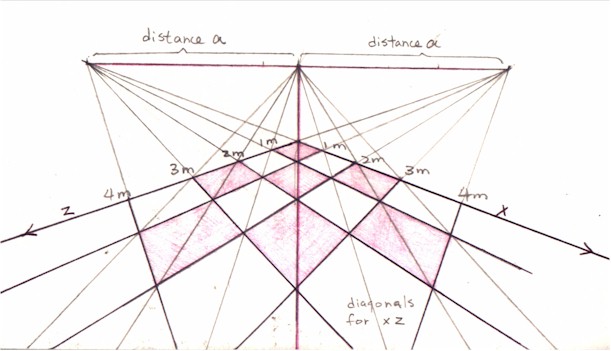
This technique is well-known. But we must find the relationships between the vanishing points for the floor plane and those for the diagonals of the two vertical wall planes.

We have so far 3 vanishing points for the floor plane.

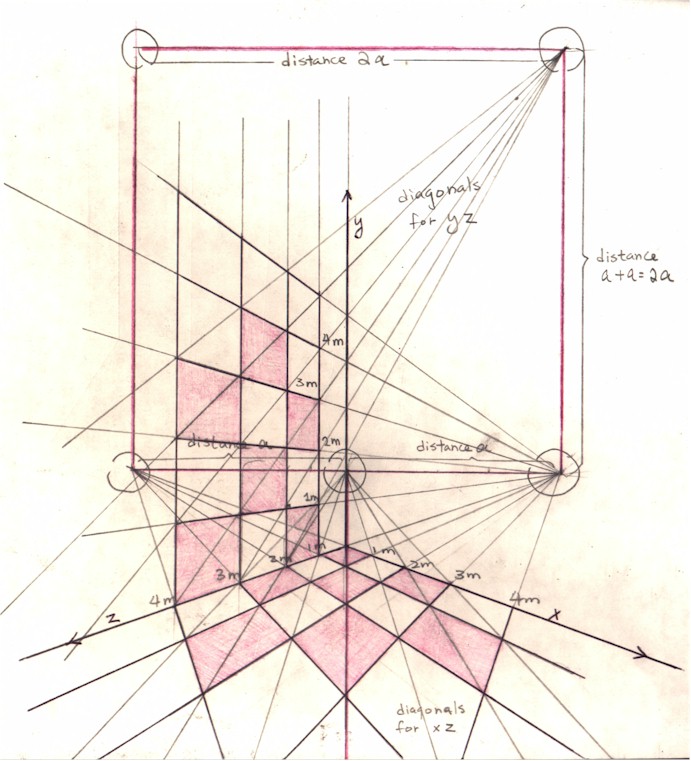
To know how high you should draw the heights of all the cubes that have each as their horizontal plane each square of the floor plane, you need to find the vanishing point for the diagonals of each of the 2 vertical wall planes (plane yx & plane yz).

The formula I’ve found for finding the vanishing point for the diagonals of the vertical plane on the left hand side (plane yz), for example, is: (1) draw a straight line that is perpendicular to the horizon and rises upward from the right-most vanishing point for the floor plane xz; (2) plot on this line a point whose distance from the right-most vanishing point for the floor plane is of the same length as the horizon (between the right-most and left-most vanishing points for the floor plane, i.e. distance a + a = 2a): this point is the vanishing point for the diagonals of the left vertical plane yz. (3) Do the same on the left side (but this step is not necessary). The 4 vanishing points (right-most and left-most vanishing points for the floor plane, and the vanishing point for the diagonals of the vertical plane on the right hand side and that for that on the left hand side) thus form a square (Figure 3). Now the volume of space is divided into cubes of equal size in linear foreshortening perspective.

Figure 3

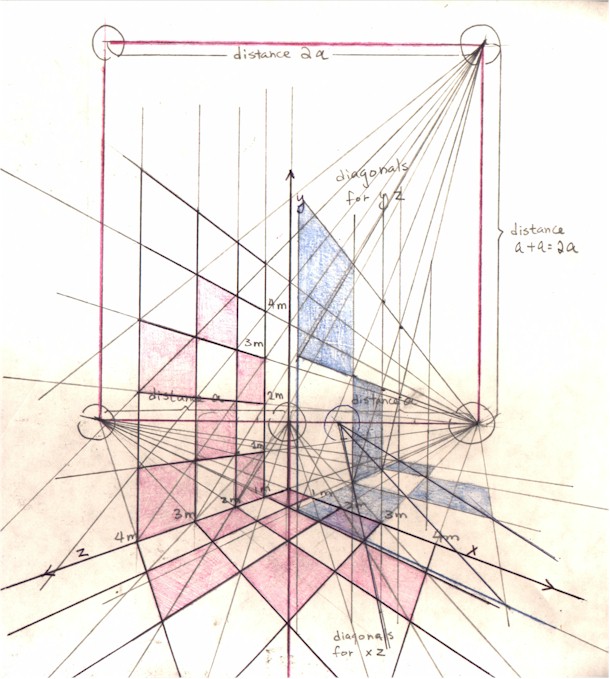
If you plot the vanishing point for the diagonals of the floor plane xz not right in the middle of the horizon line, but, for example, to the right of the middle point, this means that you have shifted your standpoint to the left, so that the angle formed by the straight line drawn from your standpoint to the intersection of the vertical planes with the left vertical plane (yz) is now less than 45 degree, and so on. But all other vanishing points would still work (Figure 4: the new foreshortening of the coordinates is shown in blue).

Figure 4

My piece "Yu Trains his Soldiers..." (2000) is done with this Formula 1. A. You can see how this drawing gradually develops:

The followings are also done with this Formula 1. A.:

Formula 1.B.

Looking Glass (1994)

Now what if there is foreshortening of the height? The "Looking Glass" on the left is done with the foreshortening of the height but with the artist-observer in the same standpoint as in Figure 1. Nothing else of Formula 1.A. changing, what you first need to do is plot the vanishing point for the vertical lines of the 2 wall planes (yz & yx). That is to say, foreshortening of height means just that the lines of the vertical planes (in the y direction) do this time converge on a vanishing point (in the case of "Looking Glass", below the horizon line). This vanishing point for the lines of y direction is to be plotted any where on the line (but below the horizon line in the present case) marking the intersection of the wall planes (i.e. the y axis itself). (Figure 5) This line marking the intersection cuts, as in Figure 2, the horizon right in half and its intersection with the horizon line is where the vanishing point for the diagonals of the floor plane xz is located. The further you plot the vanishing point for the y-axis lines away from the horizon line, the lesser the foreshortening of the height; the closer, the greater the foreshortening. In the "Looking Glass", it is plotted rather close (as is also the case in the figures below), resulting in great foreshortening from head to toes of the person.

Figure 5

|<---- a ---->|<---- a ---->| *--------------*--------------* (horizon line) | | | | | | | * <- vanishing point for lines of y axis

Remember that the vanishing point (*) for diagonals of the floor plane xz
lies still at the middle of the horizon line

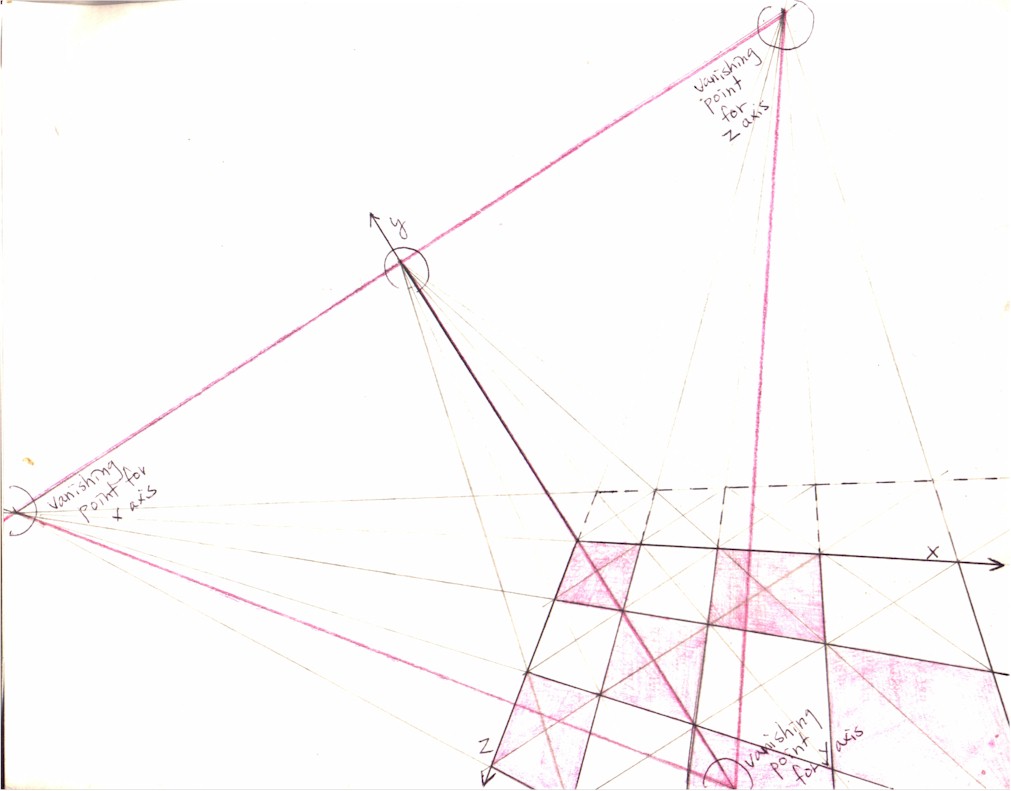
Secondly -- the crucial step -- you need to find the vanishing point for the diagonals of the vertical wall plane (say) yz. Here is the formula I've discovered: the vanishing point for the diagonals of the vertical wall plane yz is found by drawing a straight line (1) that is perpendicular to the straight line connecting the vanishing point for lines of z axis with the vanishing point for lines of y axis and (2) which passes through the point of intersection between all 3 planes of space (plane xz, yz, and xy; this point is the 0 coordinate for all 3 x, y, and z axes). This straight line will be the first diagonal for the plane yz and its intersection with the straight line connecting the vanishing point for lines of z axis with the vanishing point for lines of y axis will be the vanishing point for the diagonals of the plane yz. (Figure 6; the diagonals of the vertical wall plane yz are marked blue.)

Figure 6

The space can now be carved out into cubes of equal size (1 m x 1 m x 1 m): i.e. the three dimensional Cartesian coordinate in foreshortening including the foreshortening of height.

Formula 2.A.

Le Temps (Looking Glass 2)

Now consider that you move to a new position: a straight line drawn from this position to the intersection point of all three planes xz, xy, and yz (the 0 coordinate for all 3 axes of x, y & z) now forms a 30 and 60 degree angle with the z and x axis, respectively. (Figure 7) Now the system of vanishing points for the floor plane xz will drastically alter. In addition to this, consider that the lines of the vertical axis y are also foreshortened. “Looking Glass 2” is done with the formula for this new situation. What we have here is like the wide-angle photograph. The formula I've discovered for this standpoint of the artist (wide-angle linear perspective) can be explicated by comparison with the previous standpoint.

Figure 7

Figure 8

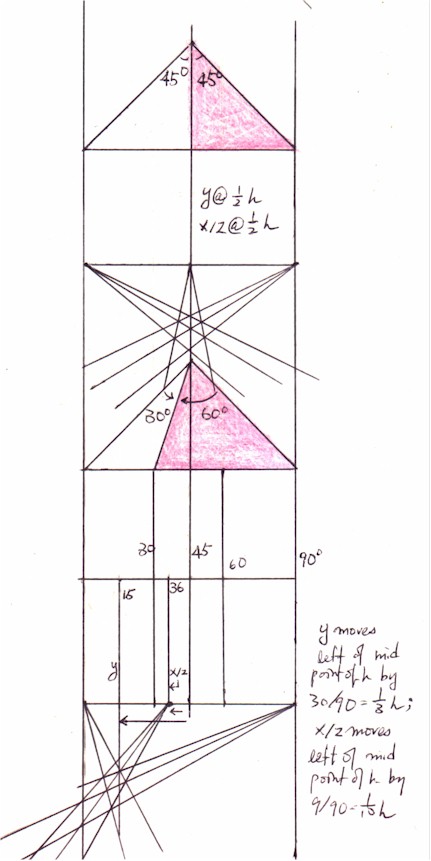
Consider Figure 8. When the standpoint (and line of sight) of the artist cuts the xz plane exactly in half (45 & 45 degree: Formula 1.B.), the y axis in the 2-D linear perspective also intersects the horizon line exactly at the middle (y @ 1/2 h; remember that in the foreshortening the y axis is always perpendicular to the horizon line). In addition, the vanishing point for the diagonals of the floor plane xz (x/z) coincides with the intersection point between the y axis and the horizon line. Moving 15 degree leftward from this standpoint (now at 30 - 60 degree) means that the y axis has to shift leftward from its original midpoint position on the horizon line by 1/3 of the total length of the horizon line (h = the length from the leftmost vanishing point for lines of x axis to the right most vanishing point for lines of z axis) -- as 15 degree is 1/3 of the original 45 degree -- and the distance of the intersection point between the y axis and the horizon line from the left most vanishing point for lines of x axis is now 1/6 of the total length of the horizon line, as 15 degree is 1/6 of the total 90 degree. In addition, the vanishing point for the diagonals of the floor plane xz (x/z) no longer coincides with the intersection point between the y axis and the horizon line. Rather, it shifts leftward only by 1/10 of the total length of the horizon line. If h is 90 (as marked in Figure 8) in length (the left most vanishing point for lines of x axis being the starting point 0), then the intersection point between the y axis and the horizon line (y) is now at 15, and the vanishing point for the diagonals of the floor plane xz (x/z) is now at 36 (45 - [90/10] = 36).

In this way the foreshortening of the floor plane xz can now be had. (Figure 10: here the length of the horizon line is marked out in centimeters to convey the positions of y & x/z.) The vanishing point for the lines of the y axis, as before, is arbitrarily chosen somewhere on the y axis below the horizon line. Just like before, the further you plot the vanishing point for the y-axis lines away from the horizon line, the lesser the foreshortening of the height; the closer, the greater the foreshortening.

Figure 9

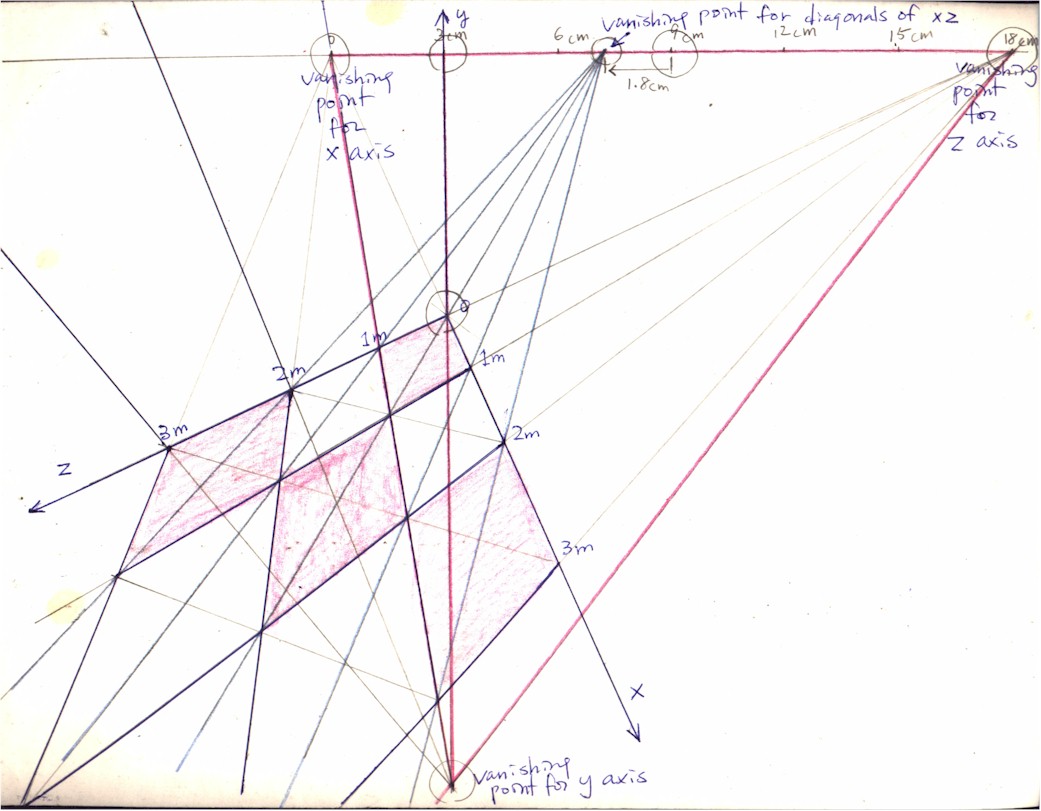
Now the vanishing point for the diagonals of the vertical wall plane yz is found just as in the previous: draw a straight line (1) that is perpendicular to the straight line connecting the vanishing point for lines of z axis with the vanishing point for lines of y axis and (2) which passes through the point of intersection between all 3 planes of space (plane xz, yz, and xy; this point is the 0 coordinate for all 3 x, y, and z axes). This straight line will be the first diagonal for the plane yz and its intersection with the straight line connecting the vanishing point for lines of z axis with the vanishing point for lines of y axis will be the vanishing point for the diagonals of the plane yz. (Figure 10; the diagonals of the vertical wall plane yz are marked red this time.)

Figure 10

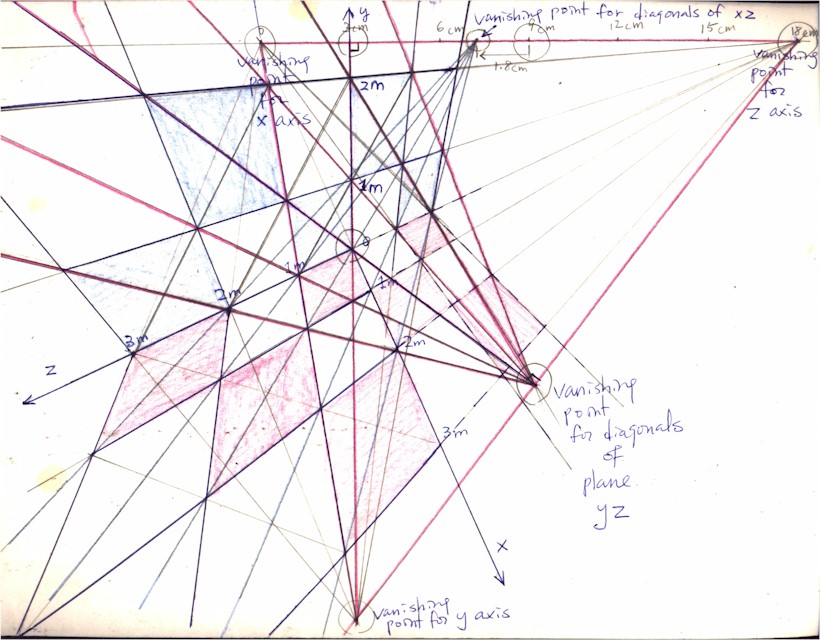
In addition to "Le Temps" "Anamnesis" (1999) is also done with Formula 2.A. (30 /60). As you can see it develop:

By Lawrence Chin. 2004.