|
Scientific Enlightenment, Div. Two
4. The Problem of Representation Chapter 1 Mathematics as Representation and the Essence of Calculus ACADEMY | previous section | Table of Content | next section | GALLERY |
|
|
Scientific Enlightenment, Div. Two
4. The Problem of Representation Chapter 1 Mathematics as Representation and the Essence of Calculus ACADEMY | previous section | Table of Content | next section | GALLERY |
Copyright 2003, 2007 by Lawrence C. Chin. This webpage is best viewed with Internet Explorer. In some browsers, such as Firefox or Safari, many of the mathematical equations below will not display correctly. In such case, please consult the PDF version of this webpage.
While the acquisition of language by the Homo species marked the beginning of one dimensional representation in animal consciousness, this representation remained qualitative. The emergence of a full-blown number system among Homo sapiens sapiens during the Neolithic Revolution, however, represented the beginning of the transition from (one dimensional) qualitative to (one dimensional) quantitative representation. The transition has been very gradual in revealing its ultimate import; it is above all a progress, since what was involved was the sharpening of an approximate representation to a precise one. The blossoming of the one dimensional quantitative representation during the age of Enlightenment – in the form of Calculus – showed the power of a quantitative representation (description) of nature.
In "The Problem of Representation" our objective is the laying-bare of the constitution of (pre-relativity) classical mechanics. We define (pre-relativity) classical mechanics by saying that it consists in the completion of the transition to precise one dimensional quantitative representation of reality, as presented in our immediate experience, in all its four dimensions. The "progress" mentioned, that is, is near its end.
The foundation of classical mechanics is laid with three contributions: the first two are Descartes': his analytic geometry and his metaphysics; and the third is Leibniz's calculus. Here we will briefly outline the meaning of analytic geometry and calculus. In the next chapter we will deal with Descartes' innovation in metaphysics as relating to the constitution of classical mechanics, and also lay out the calculus of its constitutive concepts such as force, work, and energy.
The meaning of the Cartesian revolution
To understand how a quantitative representation or description works, let us consider the calculus of a simple phenomenon of motion, the fall and retraction of a yoyo.
The phenomenon is first analyzed into components: distance (of falling), time (of falling), velocity (speed of falling in a given direction), and acceleration (change in the speed of falling). The analyzation is by no means arbitrary: the phenomenon is "cut open" along space and time – distance, representing one dimension of space (in the present case the downward and then the upward movement of the yoyo), and the time elapsed of the traveling of the yoyo. A relationship is then established between space and time in order to reintegrate them, via the concepts "velocity" and "acceleration". Thus in this manner of analyzation and integration, the phenomenon (the motion of the yoyo) can be represented quantitatively, i.e. precisely.
The analyzation first occurred at the two-dimensional plane, via the Cartesian coordinate. The representation of the motion of the yoyo on the Cartesian plane would be two-dimensionally quantitative, with space (or the one dimension of it that is involved) identified with one axis (y) and time with the other (x). (See Figure 1.)
This two-dimensional representation is then reduced to one dimension, in the medium of Descartes’ analytical geometry: p(t) = t2 - 4t + 3. This reduction or translation from the two-dimensional plane to the one-dimensional equation is the essence of Descartes’ analytical geometry. Both the parabola and the equation are quantitative, and hence precise, representation of the yoyo’s motion; and insofar as the yoyo’s position in space is taken as the center of description in both representations (the question is "What is the position of the yoyo at such specified time?") and therefore acts as the guide (p(t) =... ) in the one-dimensional equation, the components just isolated along space and time have already been integrated in each representation: the equation and the parabola at once dissect the motion of the yoyo into components (along space and time) and re-integrate them by showing the relationship of correspondence between the two components of spatial position and temporal instant. They are both representation of the whole of the yoyo's motion. At this (pre-calculus) stage, quantification is made possible by the numeralization of space and time (cutting up space and time into definite intervals to form the Cartesian coordinate) and the application of geometry to the shape represented on the coordinate to effectuate the translation. (It is presupposed, of course, that, prior to representation, the mind has already learned to "time" – quantify – the motion in the original four-dimensional medium of space-time with the help of a watch.)
This Cartesian process of translation from the two-dimensional to the one-dimensional quantitative expression is usually presented as an unification of two mathematical traditions: geometry and algebra. (Fritjof Capra, The Web of Life (1996), p. 114.) It is usually said that geometry -- in the present case the two dimensional quantitative representation on the Cartesian coordinates -- the West inherited from the Greeks, while Algebra came to Europe from the Islamic world (al jabr). In fact, the Greeks had some algebra as well, although their tendency toward "geometrization" prompted them to solve the one dimensional algebraic problems through their translation into two dimensional geometric problems. The Muslims (mostly Arabs and Persians, some Near Eastern Christians) developed some algebra themselves and learned some from the Indians. The Indians were the earliest to have developed it and they called it avyakat-ganita, "the science of calculation with the unknown". (Robert Kogan, The Alphabet Effect, p. 137) (We are tracing the lineage that led to modern European mathematics, ignoring other mathematical traditions for now, such as in China.) The one-dimensional Cartesian translation of the two-dimensional coordinate, in the form of, say, y = x2 - 4x + 3, is the higher algebraic form called "function", the ordinary being, e.g. (a + b)2 = a2 + 2ab + b2.
The earliest Hindu documentary evidence of algebra is found in the Bakhshali manuscript, discovered in 1881 in a village called Bakhshali and taken to be a copy of the fifth century A.D. original. ("The Bakhshali Manuscript", O'connor and Robertson.) The Indians having already developed zero (and the sign for it) while the Greeks never did, confusions arise in this manuscript because the notational sign for the unknown value is the same as that for zero. An example of the problem from it is:
|
"One person possesses seven asava horses, another nine haya horses, and another ten camels. Each gives two animals, one to each of the others. They are then equally well off. Find the price of each animal and the total value of the animals possessed by each person."
The solution, translated into modern notation, proceeds as follows. We seek integer solutions x1, x2, x3 and k (where x1 is the price of an asava, x2 is the price of a haya, and x3 is the price of a camel) satisfying 5 x1 + x2 + x3 = x1 + 7 x2 + x3 = x1 + x2 + 8 x3 = k. Then 4 x1 = 6 x2 = 7 x3 = k - (x1 + x2 + x3). For integer solutions k - (x1 + x2 + x3) must be a multiple of the lcm of 4, 6 and 7. This is the indeterminate nature of the problem and taking different multiples of the lcm will lead to different solutions. The Bakhshali manuscript takes k - (x1 + x2 + x3) = 168 (this is 4 * 6 * 7) giving x1 = 42, x2 = 28, x3 = 24. Then k = 262 is the total value of the animals possesses by each person. This is not the minimum integer solution which would be k = 131. If we use modern methods we would solve the system of three equation for x1, x2, x3 in terms of k to obtain x1 = 21k/131, x2 = 14k/131, x3 = 12k/131 so we obtain integer solutions by taking k = 131 which is the smallest solution. This solution is not given in the Bakhshali manuscript but the author of the manuscript would have obtained this had he taken k - (x1 + x2 + x3) = lcm(4, 6, 7) = 84. (Ibid.) |
This gives a flavor of the meaning of algebra in its first appearance. The point is to show that, unlike geometry, which is two dimensional, algebra is one dimensional representation, so that "5 x1 + x2 + x3 = x1 + 7 x2 + x3 = x1 + x2 + 8 x3 = k" is the quantitative, one dimensional way of representing the situation after the exchange of horses among the three persons. The first Arabic treatise on algebra was the one by Muhammad ibn Musa al-Khwarizmi, under the patronage of the Abbasid Caliph al-Ma'mun (813 - 33), and from whose name came the word "algorithm". "The Arabs did not know about the advances of the Hindus so they had neither negative quantities nor abbreviations for their unknowns. However al-Khwarizmi... gave a classification of different types of quadratics (although only numerical examples of each). The different types arise since al-Khwarizmi had no zero or negatives. He has six chapters each devoted to a different type of equation, the equations being made up of three types of quantities, namely: roots, squares of roots and numbers, i.e. x, x2 and numbers.
"Al-Khwarizmi then shows how to solve the six standard types of equations. He uses both algebraic methods of solution and geometric methods. For example to solve the equation x2 + 10 x = 39 he writes [in F Rosen (trs.), Muhammad ibn Musa Al-Khwarizmi: Algebra (London, 1831)]: '... a square and 10 roots are equal to 39 units. The question therefore in this type of equation is about as follows: what is the square which combined with ten of its roots will give a sum total of 39? The manner of solving this type of equation is to take one-half of the roots just mentioned. Now the roots in the problem before us are 10. Therefore take 5, which multiplied by itself gives 25, an amount which you add to 39 giving 64. Having taken then the square root of this which is 8, subtract from it half the roots, 5 leaving 3. The number three therefore represents one root of this square, which itself, of course is 9. Nine therefore gives the square.'
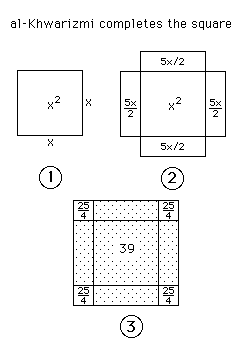"The geometric proof by completing the square follows. Al-Khwarizmi starts with a square of side x, which therefore represents x2 (Figure 1). To the square we must add 10x and this is done by adding four rectangles each of breadth 10/4 and length x to the square (Figure 2). Figure 2 has area x2 + 10 x which is equal to 39. We now complete the square by adding the four little squares each of area 5/2 * 5/2 = 25/4. Hence the outside square in Figure 3 has area 4 * 25/4 + 39 = 25 + 39 = 64. The side of the square is therefore 8. But the side is of length 5/2 + x + 5/2 so x + 5 = 8, giving x = 3." (Al-Khwarizmi, O'Connor and Robertson)
Khwarizmi's sources have been debated: Euclid's Elements, or a Hebrew text Mishnat ha Middot (ibid.), or Diophantus even. ("The Scientific Enterprise", A.I. Sabra in The World of Islam, ed. Bernard Lewis) It shall only be noted here that the "proof" is the two dimensional representation of the one dimensional quadratic equation. This is another example where we move back and forth -- translation -- between the one dimensional and the two dimensional representation. This technique -- the translation of the one-dimensional algebraic problem into two-dimensional geometrical shapes in order to solve it visually -- is the more primitive, and is widely employed earlier among the Greeks: their geometrical algebra (Greek Mathematics, Vol. I, From Thales to Euclid, with translation by Ivor Thomas, Loeb Classical, p. 187). It is more primitive because it is more concrete, i.e. it bespeaks an inability to free oneself from two-dimensional visual shapes and to work solely within the more abstract one-dimensional equation. The so-called Greek tendency toward "geometrization" in fact bespeaks their backwardness in this matter. (The Greeks resort to geometric representation even when it comes to arithmetic; e.g. they use straight lines proportional in length to the numbers to represent these numbers, and then place two such lines as adjacent sides of a rectangle which then represents the product of the two numbers. Greek Mathematics, p. 86.) Khwarizmi has made some advancement but has kept in use the two-dimensional visual representation. But the Cartesian coordinate is of a different type of two-dimensional representation. The "solution", i.e. representation, is present all at once; this is because it represents a function, which is set up to represent motion, a relationship of correlation between (the change of) space and (the change of) time. The situation that is represented is no longer static, as was before. Descartes' advancement in "geometry" consists in the enlargement of its range of representation to include one further dimension of reality, that of time. The algebraic equation from Bakhshali represents a static situation of equalization of possessions. So is the quadratic of Khwarizmi a representation of a static situation. "With Descartes' new method, the laws of mechanics [i.e. of motion] that Galileo had discovered could be expressed either in algebraic form as equations or in geometric form as visual shapes. However, there was a major mathematical problem, which neither Galileo nor Descartes nor any of their contemporaries could solve. They were unable to write down an equation describing [i.e. representing] the movement of a body at variable speed, accelerating or slowing down." (Capra, ibid., p. 115) An object moving at constant speed, without acceleration or deceleration, has the equation (i.e. the one dimensional quantitative representation) of the form of y = mx + b, whose two dimensional representation on the Cartesian coordinate would be a straight line. As seen above, the motion of variable speed is a curve on the Cartesian coordinate. Its one dimensional, algebraic representation was accomplished only with Leibniz. The specific move to this "calculus differentialis" (the final conclusion of the Cartesian revolution) will be considered later; for now it suffices to note that the analytic geometry of Descartes consists more than in the unification of geometry and algebra, more than in this simple translation from the two dimensional to the one dimensional quantitative representation, which Al-Khwarizmi has already done. The very structure of number changes with the Cartesian revolution.
Oswald Spengler has presented in Der Untergang der Abendlandes (The Decline of the West)1 an insightful delineation of the difference between the Greek tradition of mathematics in the beginning with a special focus on geometry, the "Middle-Eastern" tradition in the middle period, and the Western tradition of modern time. We must reject his thesis that the mathematics a culture invents is simply an expression of its inner soul as much as its art and architecture are -- "Mathematik ist also auch eine Kunst" (I, p. 85), he exclaims2 -- that it is consequently of the nature of an organism which goes through the stages of awakening (birth), maturation, and decline, and that the three traditions of the West therefore do not together form a linear development of progress but are incommensurable one with another just as the art forms that their cultures have invented are -- a thesis that deprives mathematical discoveries of their objectivity. We on the other hand posit precisely a linear development of progress that connects these three traditions in a logical sequence of advancement. A consequence of Spengler's thesis is that the mathematics of a given civilization fits in with its productions in other spheres, they together making manifest an "Idee" in Goethe's sense (i.e. the inner soul of the civilization) -- thus the concrete, sense-bound geometry of the Greeks fits in with the sensuous bodiliness ("sinnlich-körperhaften") of its anthropomorphic sculptures while the abstract, sense-alien geometrical analysis of the Baroque West forms a coherent package with its instrumental music and perspective in art -- such that the mathematics of every culture represents a particular Weltanschauung that is not shared by the mathematics of other cultures. This we accept. Combining our supposition of a linear development of mathematics leading up to its modern Western version with the thesis that the mathematics of a given epoch expresses a particular Weltanschauung, we thus arrive at the view that the three epochs of "Western mathematics" (i.e. mathematics as developed in the Western Ecumene as opposed to the Eastern Ecumene) -- the Greek initial, the Middle-Eastern middle, and the European modern period -- represent three different paradigms and that between them there have been paradigm-shifts in Thomas Kuhn's sense. This is what we mean by "change in the structure of number" -- a paradigm-shift -- effected by the Cartesian revolution of analytic geometry: it is not a simple amalgamation between geometry and algebra.
Classical mathematics comes to its first explicit expression, Spengler asserts, in the hands of Pythagoras, the "Islamic" (or "Magian" in his terminology, i.e. Middle-Eastern), in the hands of Diophantus, and the modern (Western), in the hands of Descartes. These are the founders of their respective paradigm. Spengler characterizes classical mathematics as "stereometric" ("solid geometry"); it is the "teaching of the relationships of magnitude, dimension, and form among fleshy bodies" ("die Lehre von den Größen-, Maß- und Gestaltverhältnissen leibhafter Körper"; I, p. 88). "Euclid, who rounded off [classical world's] system in the third century, means, when he spoke of a triangle, with the innermost necessity the boundary surface [Grenzfläche] of a body, never a system of three intersecting straight lines or a group of three points in three-dimension space" (ibid.). The thinking about numbers and geometric shapes, in other words, was still inextricably bound up with objects in immediate (functional) sense-perception.
| Deshalb ist die Vorstellung irrationaler Zahlen, in unsrer Schreibweise also unendlicher Dezimalbrüche, dem griechischen Geiste unvollziehbar geblieben... In der Tat liegt im vollzogenen Begriff der irrationalen Zahl die völlige Trennung des Zahlbegriffs vom Begriff der Größe und zwar deshalb, weil eine solche Zahl, p z. B., niemals abgegrenzt oder exakt durch eine Strecke dargestellt werden kann. Daraus folgt aber, daß in der Vorstellung etwa des Verhältnisses der Quadratseite zur Diagonale die antike Zahl, die durchaus sinnliche Grenze, abgeschlossene Größe ist, plötzlich an eine ganz andere Art der Zahl rührt, die dem antiken Weltgefühl im tiefsten Innern fremd und darum unheimlich bleibt, als sei man nahe daran, ein gefährliches Geheimnis des eignen Daseins aufzudecken. Dies verrät ein seltsamer spätgriechischer Mythus, wonach derjenige, welcher zuerst die Betrachtung des Irrationalen aus dem Verborgnen an die Öffentlichkeit brachte, durch einen Schiffbruch umgekommen sie, "weil das Unaussprechliche und Bildlose immer verborgen bleiben solle". (I, p. 89) | Therefore the representation of irrational number, the unending decimal fraction in our notation, is unrealizable for the Greek intellect. In fact in the concept of irrational number once achieved lies the full separation of number-concept from the concept of magnitude and this is because such number as p, for example, can never be defined or exactly represented by a straight line. From this it follows that, in the representation of, say, the relationship of the sides of a square to its diagonal, the classical number, which is thoroughly [of the kind of] sensible limit and enclosed magnitude, suddenly runs up against another kind of number which remains in the deepest sense alien to the classical world-feeling and is consequently feared, as if one were close to uncovering a dangerous secret of its own existence. This a strange late-Greek legend betrays, according to which the man who first brought the consideration of the irrational from hiddenness into openness perished by shipwreck, "because the unspeakable and the formless should always remain hidden." |
The order of things -- i.e. the paradigm -- remained for the Greeks the order of objects of immediate sense-perception. Irrational and negative numbers, since they do not represent any of these objects, fall outside order, belong to the realm of disorder. The Greeks similarly had no notation of zero either, and no notion of the unknown x essential to algebra. As yet unliberated from the objects of sensory perception, the Greeks could only have a concrete geometry as the representation of these objects in their presence-at-hand and a limited "geometric algebra." They subsisted on the level of the common persons, the Euclidean geometry being based on the everyday geometry of children and the uneducated (I p. 103); "for the classical man geometry and arithmetic are self-contained and complete sciences of the highest kind, both intuitive and both concerned with magnitudes that could be drawn or numbered" ("... beide anschaulich, beide mit Größen zeichnerisch oder rechnerisch verfahrend"; ibid.).
Diophantus advanced on the Greeks by conceiving algebraic solution of the unknown -- his break with the Greek paradigm prompts Spengler to class him among the emergent Middle-Eastern tradition -- but had yet to liberate himself completely from objects of immediate sense-perception: he had neither developed a notation for zero nor given negative numbers an objective status. He thus considered the equation 4 = 4x + 20 meaningless because a problem could not lead to a solution of -4 books. (J J O'Connor and E F Robertson, Diophantus of Alexandria) In this respect Indian algebra, with its explicit recognition of zero, had advanced one step further. Spengler emphasizes that Diophantus' algebra -- which comes to its maturity with Al-Khwarizmi -- represents a paradigm in between the classical and the specifically Western. "With Diophantus number is no longer the dimension and essence of plastic things [das Maß und Wesen von plastischen Dingen]... he no longer recognizes the plastic individuals [plastischen Einheiten] of Pythagorean numbers. On the other hand the indeterminateness of the unnamed Arabic number is also something other than the rule-governed variability of the later Western number, the function." ("Andrerseits ist die Unbestimmtheit der unbenannten arabischen Zahlen doch auch etwas ganz andres als die gesetzmäßige Variabilität der späteren abendländischen Zahl, der Funktion"; I, p. 99) The latter is what the Cartesain revolution initiated.
|
Die entscheidende Tat des Descartes, dessen Geometrie 1637 erschien, bestand nicht in der Einführung einer neuen Methode order Anschauung auf dem Gebiete der überlieferten Geometrie, wie dies immer wieder ausgesprochen wird, sondern in der endgültigen Konzeption einer neuen Zahlenidee, die sich in einer Ablösung der Geometrie von der optischen Handhabe der Konstruktion, von der gemessenen und meßbaren Strecke überhaupt aussprach...
An Stelle des sinnlichen Elements der konkreten Strecke und Fläche -- dem spezifischen Ausdruck antiken Grenzgefühls -- tritt das abstrakt-räumliche, mithin unantike Element des Punktes, der von nun an als Gruppe zugeordneter reinen Zahlen charakterisiert wird. Descartes hat den durch antike Texte und arabische Tradition überlieferten Begriff der Größe, der sinnlichen Dimension, zerstört und durch den veränderlichen Beziehungswert der Lagen im Raume ersetzt... Von Descartes an ist die vermeintlich "neuere Geometrie" entweder eine synthetische Tätigkeit, welche die Lage von Punkten in einem nicht mehr notwendig dreidimensionalen Raume (einer "Punktmannigfaltigkeit") durch Zahlen, oder eine analytische, welche Zahlen durch die Lage von Punkten bestimmt. Strecken durch Lagen ersetzen heißt aber den Begriff der Ausdehnung rein räumlich, nicht mehr körprerhaft fassen. (I, p. 101) |
The decisive act of Descartes, whose geometry appeared in 1637, consisted not in the introduction of a new method or idea in the domain of traditional geometry, as has always been said, but in the definitive conception of a new number-idea, which was expressed in the emancipation of geometry from the optical handling of drawings and from measured and measurable lines generally...
In place of the sensory element of concrete lines and planes -- the specific expression of classical boundary-feeling -- emerges the abstract-spatial, unclassical element of the point, which from now on is characterized as a group of co-ordered pure numbers. Descartes has destroyed the concept of magnitude and sensory dimension passed on through classical texts and Arabic tradition, and replaced them with the variable relation-values between positions in space... From Descartes onward the "new geometry" is either a synthetic work which determines through numbers the position of points in a space that is no longer necessarily three dimensional (a "manifold of points"), or an analytical one which determines numbers through the positions of points. To replace lengths with positions however means that the concept of extension is grasped purely spatially, and no longer bodily. |
The loss of geometric shapes of the concrete objects of experience in Descartes' "geometry" is due to the fact that this geometry is not devised to represent them but the relationship between space and time; i.e. the range of representation has now enlarged beyond static objects to encompass the structure of space-time, as mentioned. The essence of every one of the mathematical innovations effected by the West -- which Spengler characterizes as "new forms of number" insofar as they go beyond sensory experiences to which the classical and Arabic number-operations are confined -- consists in this enlargement of the range of representational capacity: imaginary and complex numbers, infinite series, differential geometry, the expansion of functions into series and even into infinite series of other functions, etc. If "function" is "a variable relation that is no longer confined within optical limits" ("die variable, in optische Grenzen nicht mehr einzuschließende Beziehung"; p. 104) it is because the positions in space over time cannot be visualized in a static, synchronic moment. When Spengler compares 3x + 4x = 5x with xn + yn = zn (the solutions for the latter probably exclude all integers when n > 2) and considers the latter equation as a whole (a relation) as a single number -- the new kind of number the West has invented -- because none of x, y, z, and n is confined to a single numerical value, he is drawing attention to the fact that each of these letters now can represent multiple numerical values and that the whole relation represents the same value of relation which multiple sets of numerical candidates have in common. What Spengler characterizes as a qualitative leap in the conception of number in fact is founded on a quantitative leap in the enlargement of the range of representation. Spengler concludes the essence of Western analytic "geometry":
| Die Geometrie von der Anshauung [Hellenic], die Algebra vom Begriff der Größe [Hellenistic] zu befreien und beide jenseits der elementaren Schranken von Konstruktion und Rechnung zu dem mächtigen Gebäude der Funktionentheorie zu vereinigen, das war der große Weg des abendländischen Zahlendenkens. So wurde die antike, konstante Zahl zur veränderlichen aufgelöst. Die analytisch gewordene Geometrie löste alle konkreten Formen auf. Sie ersetzt den mathematischen Körper, an dessen starrem Bilde geometrische Werte gefunden werden, durch abstrakt-räumliche Beziehungen, die zuletzt auf Tatsachen der sinnlich-gegenwärtigen Anschauung überhaupt nicht mehr anwendbar sind. Sie ersetzt zunächst die optischen Gebilde Euklids durch geometrische Örter in bezug auf ein Koordinaten-system, dessen Anfangspunkt willkürlich gewählt werden kann, und reduziert das gegenständliche Dasein des geometrischen Objekts auf die Forderung, daß während der Operation, die sich nicht mehr auf Messungen, sondern auf Gleichungen richtet, das gewählte System nicht verändert werden darf. Alsbald werden aber die Koordinaten nur noch als reine Werte aufgefaßt, welche die Lage der Punkte als abstrakter Raumelemente nicht sowohl bestimmen, als repraesentieren und ersetzen. Die Zahl, die Grenze des Gewordnen, wird nicht mehr durch das Bild einer Figur, sondern durch das Bild einer Gleichung symbolisch dargestellt. Die "Geometrie" kehrt ihren Sinn um: das Koordinatensystem als Bild verschwindet, und der Punkt ist nunmehr eine vollkommen abstrakte Zahlengruppe. ("Vom Sinn der Zahlen", 16) | To free geometry from the visual [Hellenic], and algebra from the notion of magnitude [Hellenistic], and to unite both, beyond all elementary limitations of drawing and counting, in the great structure of function theory -- such was the grand course of Western number-thought. The constant number of the Classical mathematics was dissolved into the variable. The geometry which has become analytical dissolved all concrete forms. It replaces the mathematical bodies in which rigid pictures of geometrical values are found [c.f. the example of Al-Khwarizmi], with abstract spatial relations, which in the end are no longer applicable to the visual phenomenon present to the senses in the immediate moment. It firstly replaces the optical figures of Euclid with geometrical loci in reference to a coordinate system, whose beginning point can be arbitrarily chosen, and reduces the object-like existence of geometrical objects to the condition, that, during the operation, which is no longer directed toward measurement, but toward equation, the chosen system should not be changed. But these coordinates are immediately regarded as pure values, which not so much determine as represent and replace the positions of points as abstract spatial elements. Number, the boundary of things-become, is presented, no longer as the [magnitudinal] picture of a figure, but symbolically as the [relational] picture of an equation. "Geometry" has changed its meaning: the coordinate system disappears as a picture, and the point is now a perfectly abstract number-group. |
This characterizes the evolution of quantitative representation from the functional to the structural perspective. Function is therefore not simply algebraic in the traditional sense, but a specially evolved form of it, which, together with its two dimensional correlate, the more abstract geometry of a spatial system of relations between points, comes to be as demanded by the contraction of the temporal succession of sense-perceptions (rather than a single, present sense-perception) into a single-moment representation of two and one dimension. Geometry is no longer the representational measurement of magnitudinal spatiality (to which even motions, such as the orbits of the planets, are reduced in the functional perspective, as in the Ptolemean), but representation of the internal relational structure of motion, a real unity of space and time. This internal relational structure of temporal succession, as for example manifested in the changing speed, is information already contained in the earlier example, in the representation p(t) = t2 - 4t + 3 with its corresponding curve, thus showing how an equation of physics is a manner of representation. Let us then continue on this point.
The meaning of the representation of motion by calculus
Although the one-dimensional quantitative representation obtained above (the equation) is already an integral description of the phenomenon in question – i.e. the components analyzed have already been integrated -- this phenomenon of motion can be understood deeper – grasped even more precisely – by further developing the integration, by soliciting out more information on the relationship between the two axes which still lies hidden in the figure of the parabola. It is Leibniz with his invention of calculus who has made this possible, and therefore completed the Cartesian revolution. We are referring to the calculation of "velocity" and "acceleration."
Velocity is thus a composite concept of space and time: it relates these two components. It is: distance traveled over time elapsed. (This is its qualitative definition, i.e. representation – in the one dimension of language, of course.) It is represented, quantitatively and "equationally" (in one dimension) as:
| v(t1) = |
lim
Dt->0 |
p(t1 + Dt) - p(t1) Dt |
i.e. |
distance travelled time elapsed |
Or the derivative of the representation of position:
Velocity (again to represent it qualitatively in the one dimension of language) is the rate at which the position of the yoyo changes at the instant t1.
The formula is derived this way (following Alexander Hahn, Basic Calculus):
p(t1) = position of the yoyo at time t1;
Dt = time elapsed;
t1 + Dt = the new time;
p(t1 + Dt) - p(t1) = change in position or distance travelled over the time interval between t1 and t1 + Dt;
|
p(t1 + Dt) - p(t1) Dt |
= distance travelled divided by time elapsed |
Acceleration is a composite of velocity and time, and hence of space/time and time. It is the representation of the change in velocity over time elapsed; that is (to represent it qualitatively, in one dimension), the rate at which velocity changes at the instant t1.
| a(t1) = |
lim
Dt->0 |
v(t1 + Dt) - v(t1) Dt |
i.e. |
change in velocity time elapsed |
Or the derivative of velocity:
The quantitative one-dimensional representation of the yoyo in motion is now complete. It is (position-centrically speaking) p(t) = t2 - 4t + 3, with v(t) = 2t – 4 and a(t) = 2. This representation of the yoyo in motion is precise, and no longer a mere approximation as in a word-description of the same motion (which is one-dimensional and qualitative: e.g. "The yoyo moves fast up and down!"). In being precise, it captures something like the structure of the motion of the yoyo. It represents the “whole” of the motion, but also its structure. Thus any moment of the drawn-out motion of the yoyo – a cross-section of the whole, so to speak – can be described – represented – quantitatively (precisely) by plugging into the “structure” (the equation) the quantitative representation of the "moment" in question: at time 0 (t = 0: the quantitative representation of the moment), yoyo’s position is p(0) = 02 - 4 * 0 + 3 = 3; v(0) = 2 * 0 – 4 = -4 (or an absolute speed |-4| = 4 feet/ second in the downward direction; a(0) = 2 feet/ square second. This is the meaning of the "prediction" of the equation.
The evolution of representation
Needless to say, these two representational techniques developed by the mathematicians -- the Cartesian coordinate as the two dimensional quantitative representation and the equation of calculus as the one-dimensional quantitative representation -- are not our ordinary ways. In everyday life we would represent the yoyo's motion (which is a four-dimensional phenomenon, to be sure, with three dimensions of space plus one dimension of time), although also one- and two-dimensionally, but qualitatively. Our qualitative one-dimensional representation of the yoyo's motion would be our linguistic description of it, as said: "The yoyo was released, descended rapidly until it came to a halt, and then ascended back up." Qualitative, and so less precise, is this because no numbers are involved: a mere approximation. Our qualitative, two-dimensional representation of the yoyo's motion would be the drawing of it, as in Figure 2, but without the number grid that measures the depth of yoyo's descent and the height of its ascent and without the timing that measures the time elapsed during the descent and the ascent. (Be sure to take the 0 on the distance-grid as indicating some sort of horizon, perhaps the sill of the window out of which the hand extends to release the yoyo.)
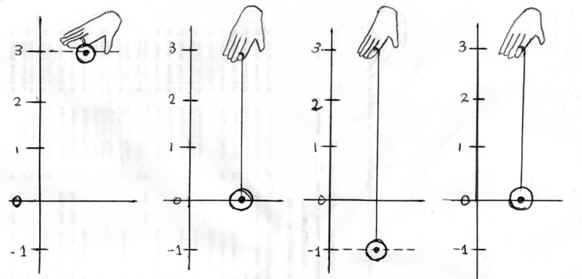
time= 0 second time= 1 second time= 2 second time= 3 second |
time= 4 second
|
The drawing above, if without the number grids and timings, also only represents the yoyo's motion qualitatively. But with the grids and timings, it is a mixture of the quantitative and the qualitative, as is the modified linguistic statement: "The yoyo was released at 0 second, reached a depth of 3 feet down at 1 second, then came to a halt at 2 second at 1 foot below the horizon..." These sorts of mixtures are representations frequently used in science lectures or police reports, etc.
Other than these natural capacities for language and art as our native ways of one- and two-dimensional qualitative representation of the four-dimensional nature around us, our biological constitution gives us other means of representation as well, means that, unlike language and art, we shared with other sentient animals: vision is a three-dimensional representation (two dimensions of space and one dimension of time), which the film represents in the same dimensions but which art represents one-dimension less; touching is a four- and hence equal-dimensional representation of nature; but then emotion -- it does represent nature in some way by capturing the mood of the latter, but in a zero-dimensional way, as a singularity, so to speak. Emotion is in fact represented in language or otherwise not through the reduction of dimensions, as commonly, but via the expansion of dimensions (e.g. a linguistic representation of it as in "I feel like floating on air when I walk on this street" is one dimension larger than the zero-dimension of emotion.) Of all the means of representation emotion is certainly the most imprecise.
If sentient beings or consciousness is regarded as Universe's way of becoming conscious of itself, then representation is the means of this (self-)consciousness; it is the framework where consciousness occurs. The progress in the evolution of consciousness is toward more accurate awareness of Reality, and we have said that this progress has been made through the stratification of Reality, through the transition from the functional to the structural perspective. Now parallel to this transition has been consciousness' progress in the precision of representation of Reality. And this progress in precision has universally involved the gradual reduction of dimensions and the move from qualitative approximation to quantitative precision. As the earliest sentient beings represented their surroundings through touch (qualitative four-dimensional: Cnidarians, e.g. the jelly fish, at the very beginning of the animal kingdom around 600 million years ago, were the first to develop a nervous system [as yet un-centralized] that permeated their tentacles with which they captured prey to put into their mouth), the later ones were able to represent through vision (qualitative three-dimensional), which increased the range, quality, and precision of representation. (Primitive eyes were first formed on flat worms some 500 million years ago; eyes continued to develop in the vertebrates through the fishes, and by the time the "four-legged fish" Ichthyostega went on land 350 million years ago eyes were fully developed on it.) This is the stage of animal, sensual consciousness (sensory informational closure). As speech started developing in the Homo lineage, in the late archaic Homo sapiens the command language of the ancestors (language composed of imperative forms only) transited to the grammatical, narrative language that we possess today (language with indicatives), so that representation (which is the meaning of narration) was further reduced to one-dimension (but still qualitative) from the three-dimension of vision. Homo sapiens sapiens also possess artistic ability, which is two-dimensional qualitative. With each reduction in dimension, the range of representation is increased, and, moreover, Reality is dissected into component parts, analyzed, and reintegrated, its structures now becoming visible. This is especially true of language.
The transition from the qualitative to the quantitative then occurred during the Neolithic Revolution, with the onset of agricultural subsistence, when the number system in language became full-blown: numbers now went beyond 3 to reach 10, 20, 50, 100. In the languages of the primitive hunter-gatherers, numbers often did not go beyond 3, with only "one", "two", and "many", so that "one, two, and many zebras" was their qualitative, im-precise, approximate representation of the herd of 22 zebras that they saw. The agriculturalists of the Neolithic, on the other hand, could begin to represent precisely by saying "22 zebras." (C.f., Merritt Ruhlen, On the Origin of Language, p. 31: "In many hunter-gatherer societies -- which included all of mankind until about 12,000 years ago -- numerals are limited to 'one', 'two', and 'many', a trait preserved by Australian languages to the present day." Or Joseph Greenberg, "Relative Pronouns and P.I.E. Word Order Type" in Language Typology 1987, p. 124: "For speakers of Proto-Eurasiatic, we must assume a hunting and food-gathering population who on the basis of the ethnographic evidence would probably not have separate, or at least, historically stable numerals above three, four, or five.")3 Nature has come a long way to acquire fully precise representation of itself.
As mathematics developed throughout the eras as an one-dimensional representation, it never yet reached the stage of being able to represent Reality in all of its four dimensions, until the invention of calculus by Leibniz in the 1600s. This is why calculus was such an important moment in the evolution of consciousness: motion (i.e. the fourth dimension, the axis of time) could now be represented, so that nature in all its four dimensions (three dimensions of space and one dimension of time) at last entered into the realm of quantitative representation by consciousness. (We are leaving aside the messy issue of contemporary awareness by physicists of extra dimensions revealed on the sub-atomic level.) From now on Nature is being represented with absolute precision through one-dimensional quantification. Mathematics is the highest form of representation. The significance of the Cartesian coordinate at this time was its role in providing the stepping stone toward the representation of motion: first representing the time-axis extraneously as the second dimension (the x axis) in a two-dimensional quantitative representational schema, then allowing the brilliant mind of Leibniz to figure out the way to fold the second dimension into the one dimension of the mathematical equation (velocity as the derivative of position). To be sure, the advancement of mathematics in the classical Arab world seems also to be in the direction of gradual reduction of dimensions, so that a century or so after al-Khwarizmi there was al-Karaji (born 953) who "is seen by many as the first person to completely free algebra from geometrical operations and to replace them with the arithmetical type of operations which are at the core of algebra today. He was first to define the monomials x, x2, x3, ... and 1/x, 1/x2, 1/x3, ... and to give rules for products of any two of these. He started a school of algebra which flourished for several hundreds of years. Al-Samawal, nearly 200 years later, was an important member of al-Karaji's school. Al-Samawal (born 1130) was the first to give the new topic of algebra a precise description when he wrote that it was concerned: '... with operating on unknowns using all the arithmetical tools, in the same way as the arithmetician operates on the known.'" ("Arabic mathematics : forgotten brilliance?", O'Connor and Robertson) The Indians, of course, being the originators of algebra, had arrived at one-dimensional representation: but the representation of all these geniuses is of the static situations, of the three dimensions of Reality only, not yet four. The Cartesian revolution is a leap beyond them, as analyzed. The one-dimensional quantitative representation through numbers, then, since the Neolithic Revolution, started from counting many things, i.e. from a static simple representation of how many things; through the more complex, but still static representation of how many and how much, this time the quantity being represented already unknown; to the dynamic representation of all four dimensions of Reality where the unknown, but represented, quantity is a relationship between and involving spatial and temporal variables. In the European lineage the reduction continues and is completed with Joseph-Louis Lagrange's Mécanique analytique (1788) where the laws of motion are completely represented by the algebraic, one-dimensional equations and from which all two-dimensional geometric forms are banished. We will elaborate on the details of this history later on in the exposition of the evolution of quantitative representation from the functional to the structural perspective: the birth of classical mechanics.
The function of numbers in the primordial disclosure of the world
To say that numbers and their operations which constitute mathematics are a form of representation is to adhere to the derivative level of truth-function, adaequatio intellectus et rei, or discovering (Entdecktheit) in Heidegger's analysis of Da-sein in Being and Time. But all forms of representation that have been noted so far, from emotion through language and art to mathematics, insofar as they are part of the activity of Da-sein (surviving and religiousness among the primitives, and self-interpretation among the modern), also have the primordial function of disclosure (Ershlossenheit). The function of numbers in representing "how many" is thus built upon their having already disclosed a quantitative version of "many". Heidegger did not in his classic give an account of the disclosive function of numbers, but Spengler did indirectly in his. When Spengler argues that a number system or a mathematics is, like all other fields of knowledge, not the representation of an objective, immutable reality but merely an expression of the inner soul of a culture, merely a part of its paradigm, he has necessarily to acknowledge the disclosive function of this number system or mathematics since the different paradigms are in effect the different results of the different disclosive activities (Da-seins). Only as a form of disclosure can Euclidean geometry be pre-figured in classical ornaments or the calculus of the infinitesimal in Gothic architecture before their birth (I, p. 81). Spengler is wise in noticing that the mathematics of a culture figures as part of its Lebensgefühl (life-feeling) which is manifested in its art, literature, music, even in its city-planning -- because this Lebensgefühl is its peculiar disclosure of the world.
When agricultural tribal peoples first became able to count 22 zebras, for instance, they had disclosed a particular dimension of Reality, its quantitative, precise dimension: the world now appeared to them differently than to the hunter-gatherers to whom, because they had no numbers beyond 3, 4, or 5, the quantitative aspect of Reality -- such as the 22 zebras -- was a mere undifferentiated confusion, i.e. remained undisclosed or concealed. When the European physicists became able to represent motion through differential equations, they had brought out more of the quantitative aspect of Reality from concealedness into clearing -- the quantitative aspect that remained concealed from the lay persons and people of other cultures.
The disclosive function of mathematical equations (i.e. representations) of motional reality (i.e. Reality in all its four dimensions) is what is referred to earlier as their Platonic eidetic function: mathematical equations as the eidoi that allow motional reality to show itself as it is, quantitatively. When Galileo decomposed the curvilinear motion of a canon ball into a vertical and a horizontal component, he was trying to get at the individual eidoi that showed up in community in the singular motion of the canon ball and which allowed this motional reality to show itself as it was quantitatively. Equations are the equivalent of the function of Being in Heidegger's Dasein-analytic and our measuring and decomposing the motional reality and devising equational representation of it is part of our Da-sein activities. What is specifically different with this doing of mechanics and with these mathematical or numerical eidoi showing themselves in motional reality is that they allow Reality to show itself in its present-at-hand quantitative precision. When we in our next chapter introduce the basic notions of classical mechanics such as work, energy, and force, we are providing the basic eidoi that so allow. The "problem of (mathematical) representation" is the problem of how such specifically advanced mode of being for quantitative, precise, and decontextualized Weltlichkeit is arrived at. In the following we will have a specific focus on the most important eidos of all, that of conservation. We will then see how the application of these eidoi for the quantitative, precise disclosure of motional reality as presented in our immediate experience to the microscopic and macroscopic reality beyond this immediate experience will constitute the modern version of the Platonic flight out of the cave of illusion.
Footnotes:
1. Der Untergang des Abendlandes, Vol. I & II, C.H. Beck'sche Verlagsbuchhandlung, München, 1923.
2. "Damit tritt der geborene Mathematiker neben die großen Meister der Fuge, des Meißels und des Pinsels, die ebenfalls jene große Ordnung aller Dinge, die der bloße Mitmensch ihrer Kultur in sich trägt, ohne sie wirklich zu besitzen, in Symbole kleiden, verwirklichen, mitteilen wollen und müssen." ("And so the born mathematician takes his place next to the great masters of the fugue, the chisel and the brush, who want also to -- and must -- clothe that grand order of things in symbols, actualize it and communicate it -- that order of things which the ordinary people of his culture bear with themselves without effectively possessing it"; I, p. 84.)
3. Note however the binary system used by a few groups of Australian aborigines :
|
Urupum 1
Okosa 2 Okosa-Urupun 3 Okosa-Okosa 4 Okosa-Okosa-Urupun 5 Okosa-Okosa-Okosa 6 Whereas the above is the additive process that is the essence of modern binary arithmetic, there is a difference which is essentially the difference between primitiveness in numeration and sophistication. These aborigines do not reckon beyond six; everything from seven to seven million is just “many” or “very many.” (Elman Service, The Hunters, 2nd ed., 1979, p. 61.) |
| ACADEMY | previous section | Table of Content | next section | GALLERY |