
|
Scientific Enlightenment
2. A. 4. The Problem of Representation (and the Constitution of Classical Mechanics) Chapter 3 Calculus and the Basic Notions in Classical Mechanics ACADEMY | previous section | Table of Content | next section | GALLERY |

|
Scientific Enlightenment
2. A. 4. The Problem of Representation (and the Constitution of Classical Mechanics) Chapter 3 Calculus and the Basic Notions in Classical Mechanics ACADEMY | previous section | Table of Content | next section | GALLERY |
| In einer berühmt gewordnen Rede sagte Helmholtz 1869 "Das Endziel der Naturwissenschaft ist, die allen Veränderungen zugrunde liegenden Bewegungen und deren Triebkräfte zu finden, also sich in Mechanik aufzulösen." In Mechanik, das bedeutet die Zurückführung aller qualitativen Eindrück auf unveränderliche quantitative Grundwerte, auf Ausgedehntes also und dessen Ortveränderung; das bedeutet weiterhin... die Zurückführung des Naturbildes auf eine einheitliche, zahlenmässige Ordnung von messbarer Struktur. Die eigentliche Tendenz aller Mechanik geht auf eine geistige Besitzergreifung durch Messung; sie ist deshalb genötigt, das Wesen der Erscheinung in einem System konstanter, der Messung restlos zugänglicher Elemente zu suchen, deren wichtigster nach der Definition von Helmholtz mit dem -- der Sphäre des Lebens entnommenen -- Worte Bewegung bezeichnet wird. | In a lecture of 1869 that has become famous, Helmholtz said "The final end of natural science is to discover the motion underlying all changes and the motive forces thereof, thus to resolve itself into mechanics." "Into mechanics", that means the referring of all qualitative impressions [data] back to the unchanging quantitative base-value, to the extended and the change of place thereof; that means furthermore... the referring of the nature-image [the empirical, seen Reality] back to the unified/ single, numerical order of measurable structure. The peculiar tendency of all mechanics consists in the intellectual conquest through measurement; it is therefore obliged to search for the essence of phenomena in a system of elements that are constant and completely accessible to measurement, and of which the most important, according to Helmholtz' definition -- speaking from the sphere of everyday life -- is designated by the word motion. |
In addition to the first (the realization that the things formerly considered independently existing -- like the solid or liquid states of matter -- are only effects of an underlying structure) -- the beginning of the structural perspective is marked by a second characteristic: the quantitative precise representation of the (Heraclitean) flux of Reality. As we have seen, the functional perspective has attempted such also, but never quite successfully, the most complete attempt being the Yijing metaphysics of Sung Dynasty, China. Another example would be Ptolemy's Almagast. Quantitative representation of Reality -- the reduction of the cosmos into numerical, and so precise and unambiguous, relations -- is therefore not the unique invention of the era of structural perspective, although it does reach -- in its fantastic success, in combination with structures, from Newtonian-Maxwellian through relativity, quantum mechanics and field theory, to the superstring -- something magnificently important. The beginning is modest, however, more or less the quantitative formulation of the common sense of everyday experience which is almost the same as in the beginning of the functional perspective, the middle part, the enlightenment of the functional perspective (philosophies), being erased from memory. This beginning is classical mechanics, which Spengler describes above: the absolute space as the immutable container in which extended objects trace out their trajectory (change their place -- motion) as absolute time passes -- uniformly at all places. A most simplistic conception of Reality, but then perhaps the most basic (and so necessary) of it.
As we have seen, Descartes laid the foundation for classical mechanics with analytic geometry which first of all represents, quantitatively (precisely) but geometrically (visually), the place-changing of something on the two-dimensional Cartesian coordinates that cut open the place-changing along the space and time axes, and then translate this, through analytic geometry, into the one-dimensional, quantitative (precise) representation that specifies, in one dimension (equation), the unchanging relationship between the spatial component and the temporal component of the phenomenon in terms of a function, y = mx + b or f(x) = ... Descartes also laid the foundation for classical mechanics in another way, in his new metaphysics: by positing the essence of matter in extension. This is necessary because the worldview of classical mechanics as described above would not be possible without stripping entities of their readiness-to-hand (Zuhandenheit) to reveal their presence-at-hand (Vorhandenheit). The invention of calculus by Leibniz -- division and infinite additions of the infinitesimals within this relationship between x and y -- in this respect, made mechanics possible, the one-dimensional quantitative representation of motion. In this chapter we shall as preparation for our study of classical mechanics lay bare its metaphysical presuppositions and basic concepts along with the mathematical tools (the basic calculus) used to represent them.
Classical mechanics, as seen above, with its reduction of the world of multifarious phenomena to the common level of things extended and changing place, presupposes the most extreme decontextualization of the world or worldhood (Weltlichkeit). This Descartes' new philosophy (Principia Philosophiae) furnishes, as Heidegger has noted (Sein und Zeit, p. 89). With Descartes, indeed, Western consciousness has attained a new level of abstraction. "Substance" is the term he uses to designate anything existent such as has been decontextualized or deprived of its readiness-to-hand. Substance is defined as something existent in itself, and all things in the universe are classified into three categories: God, consciousness (ego cogito), and material things (res corporea). Classical mechanics concerns itself only with the last of the three. Res corporea is defined by -- reduced to -- one pre-eminent property which constitutes its nature and essence, and to which all the rest are referred (sed una tamen est cuiusque substantiae praecipua proprietas, quae ipsius naturam essentiamque constituit, et ad quam aliae omnes referuntur; SZ, p. 90). This property is extension in length, breadth, and thickness (extensio in longum, latum et profundum). That is, after things in the world around us -- this thing as chair and that thing as hammer -- have been abstracted to the extent of completely shedding their equipmentality -- this its chairness and that its hammerness -- only a few characteristics are left of them, of which the most basic is their spatial dimension or extension. The other determinations (Bestimmtheiten) of substance, foremost divisio, figura, motus can be understood as modes of extension, but extensio sine figura vel motu remains on the other hand understandable (SZ, ibid.). Further, the other qualities left of things so abstracted are dispensable without the perception of the things being altered, and hence inessential, such as hardness (durities), weight (pondus), color. The example Descartes has provided is hardness:
Nam, quantum ad duritiem, nihil aliud de illa sensus nobis indicat, quam partes durorum corporum resistere motui mannum nostrarum, cum in illas incurrunt. Si enim, quotiescunque manus nostrae versus aliquam partem moventur, corpora omnia ibi existentia recederent eadem celeritate qua illae accedunt, nullam unquam duritiem sentiremus. Nec ullo modo potest intelligi, corpora quae sic recederent, idcirco naturam corporis esse amissura; nec proinde ipsa in duritie consistit.For, as far as hardness is concerned, the sense shows us nothing else about it than that portions of hard bodies resist the movement of our hands when they come up against those portions. For, if whenever our hands are moved toward a certain portion, all the bodies there should retreat with the same velocity as that with which our hands approach, we should never feel any hardness. Nor is it in any way intelligible that bodies which thus recede should accordingly lose their corporeal nature; hence this does not consist in hardness.
Consciousness, which Descartes, yet freed from the functional perspective, takes as independently existing, constitutes a second type of substance because it has no extension. Strictly speaking, only the third type of substance, God, is truly a substance, since only God truly exists in itself, without need of anything else, whereas "indeed we perceive that no other things exist without the help of God's concurrence" (alias vero omnes (res), non nisi ope concursus Dei existere percipimus). As Heidegger has noted, there is thus in Descartes' metaphysics a defect -- that cogito and res corporea aren't real substances per definition -- which he leaves as unrepairable but for which the Scholastics have long ago provided a fix. Nevertheless, Descartes' metaphysics must be considered as the foundation of a new epoch in human consciousness insofar as it has prepared for European consciousness a world of things possessed of no qualitative values but only of the quantitative value of extension, so that a purely quantitative perception and description of them as extended objects' changing place within an extended container -- classical mechanics -- can take place.
Function (in this mathematical context) is a specific type of relationship between x and y in that here for every x there is only one y that would satisfy the equation. That is, for every independent variable (x) there is only one dependent variable (y). In this way, a circle (on the Cartesian coordinate) is not (cannot be translated into) a function. But y = x2 or f(x) = 3x - 7 is. The general form f(x) = mx + b is a linear function, i.e. m and b are constants. But f(x) = b, where b = any constant, this is constant function; e.g. f(x) = 6 or g(x) = -7. In terms of mechanics, i.e. in its representation of the flux of Reality as motions of spatially extended objects through absolute space during the passage of absolute time, where x represents time and y space (place), the assumption is of course that one thing cannot be at two places at the same time. The question is whether Reality really is like this, a function. It will have important bearing on the truth of existence and human enlightenment.
Laplace remarks in Exposition du système du monde:
Le temps est pour nous, l'impression que laisse dans la mémoire, une suite d'événemens dont nous sommes certains que l'existence a été successive. Le mouvement est propre à lui servir de mesure; car un corps ne pouvant pas être dans plusieurs lieux à-la-fois, il ne parvient d'un endroit à un autre, qu'en passant successivement par tous les lieux intermédiaires. Si, à chaque point de la ligne qu'il décrit, il est animé de la même force; son mouvement est uniforme, et les parties de cette ligne peuvent mesurer le temps employé à les parcourir. (Edition of 1835, p. 29.)
"Time is for us the impression which a series of events of which we are certain leaves in our memory, that existence has been successive." This approaches an explanation of time as a purely psychological phenomenon: we think time exists because of the limitation of our experience, e.g. that we can only remember the past and not the future. "Motion is proper to serving as the measure for it; for a body, not being able to be in several places at the same time, cannot go from one place to another, save by passing through successively all the intermediary places. If, at each point of the line which it traces out, it is animated by the same force, its motion is uniform, and the components of this line can measure the time it takes to traverse them." The principle of mechanics: space, time, place-changing during time elapsed. Thus the "self-evident principle" of a thing being only at one place at one time is said by Laplace to be the foundation of the psychological experience of motion and so of time. This principle is supposed to be self-evident because the supposedly rational mind from the Cartesian era until the height of classical mechanics presumes that nature necessarily practices minimalism -- hence a thing will be at one and only one, instead of two or however many, place at one time -- which principle, as said, also underlies Fermat's law of least time for light (that, of all paths, light always chooses the path of least time in traveling from point A to B) and William Hamilton's law of least action (that the path a particle takes is always the path of least action). We know today from quantum theory that reality seems to be just the opposite -- that a subatomic particle, before observation, always takes all paths at once and seems to be at all places in the Universe at the same time: maximalism. This is in fact more rational, more logical, since minimalism presupposes that nature should choose, i.e., the minimal out of all possibilities, whereas maximalization does not entail the extra burden of "choice". Everything is simply everything; there is no logical reason why nature should make choices among everything. Again, the point is that classical mechanics (and so contemporary common sense) is illogical and quantum theory logical.
A curve, as we have seen, on the Cartesian coordinates representing the trajectory, the change of place of something, the slope (m) of a tangent (p) at point x at this curve represents then the velocity -- the rate of place-changing -- of the something at position x during time t (the x corresponding to the y), and it is calculated as the derivative of x, mp = dy/dx. This is differentiation, y/x. We have described that velocity, as the slope of the tangent or derivate, relates and integrates into a composite the spatial and temporal dimensions of an object dissected out of it, but by more than simply relating the two at corresponding points formed by the intersection of vertical and horizontal coordinates, as d'Alembert's description of the analytic geometric representation of motion would make it clearer:
Or l'analogie qu'il y a entre le rapport d'une telle ligne, & celui des parties de l'espace parcouru par un corps qui se meut d'une maniere quelconque, peut toujours être exprimée par une équation: on peut donc imaginer une courbe, dont les abscisses représentent les portions du tems écoulé depuis le commencement du Mouvement, les ordonnées correspondantes désignant les espaces parcourus durant ces portions de tems: l'équation de cette courbe exprimera, non le rapport des tems aux espaces, mais, si on peut parler ainsi, le rapport du rapport que les parties de tems ont à leur unité, à celui que les parties de l'espace parcouru ont à la leur. Car l'équation d'une courbe peut être considerée, ou comme exprimant le rapport des ordonnées aux abscisses, ou comme l'équation entre le rapport que les ordonnées ont à leur unité, & le rapport que les abscisse correspondantes ont à la leur. (Traité de Dynamique, p. viij)"Now the analogy which exists between the relationship of such line [the uniform line of time], and that of those parts of space traversed by a body which moves in a certain manner, can always be expressed by an equation: one can therefore imagine a curve, of which [the horizontal coordinates] represent the portions of time elapsed since the beginning of motion, and the corresponding [vertical] coordinates designate the space traversed during these portions of time: the equation [a function] of this curve will express, not the relationship between time and space, but, if one may thus speak, the relationship between the relationship which the parts of time have with their whole, and the relationship which the parts of space traversed have with theirs. [This is the nature of mp as representing velocity.] For the equation of a curve can be considered, either as expressing the relationship of the vertical coordinates to the horizontal, or as the equation between the relationship which the vertical coordinates have with their whole, and the relationship which the corresponding horizontal coordinates have with theirs."
For a linear function, f(x) = mx + b, the tangent p to the line (that satisfies [corresponds to] the equation) at the point (x, y) on it is just the line itself, therefore mp = m of the mx + b. For example, the function f(x) = 2/3x - 4/3 (which, with f(x) = y, may come from 2x - 3y - 4 = 0 or 3y = 2x - 4 or whatever), whose translation into 2 dimensional geometric (visual, pictorial) representation would be:

It has the slope 2/3, meaning that for every increase of 1 unit in the x-coordinate there is an increase of 2/3 in the y-coordinate, calculated by choosing any points P1 = (x1, y1) and P2 = (x2, y2) and then obtaining the proportion between the increase in y and that in x through (y2 - y1)/(x2 - x1). (Ibid.) We can easily see why velocity, being the rate at which the change of place (y coordinate) occurs at time t (x coordinate) and so obtained by distance traveled over time elapsed, becomes represented by the slope of the tangent. Leibniz's invention of "calculus differentialis" during the 1680s started with finding the slope mp of the tangent at point P of the curve,
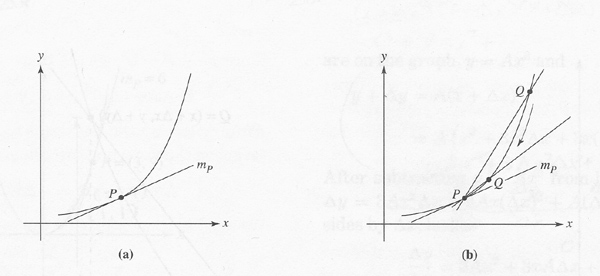
by positing another line intersecting on P and Q and then pushing Q towards P, so that "as Q closes in on P, the line through P and Q closes in on the tangent line at P", and "the slope of the line through P and Q homes in on the slope mp of the tangent." (Ibid.) Translating into the 1 dimensional (algebraic) equation, letting therefore P = (x, y) and Q = ((x + Dx), (y + Dy), the progressive approximation of the slope of the line PQ toward mp of the tangent is represented firstly as:
|
(y + Dy) - y (x + Dx) - x | = | Dy Dx | and then as | lim Dx -> 0 | Dy Dx |
= mp |
With the pushing of Q towards P represented by Dx being pushed to 0. Leibniz was able to derive a general formula for finding the slope of the tangent called the derivative by working with y = x2 along this reasoning. So if point P on this parabola be (3, 9) and Q (3 + Dx, 9 + Dy), for Q then, 9 + Dy = (3 + Dx)2 = 32 + 2*3Dx + (Dx)2. Subtracting 9 from both sides and then dividing them by Dx, we have Dy/Dx = 6 + Dx, and, with Dx pushed to 0,
| lim Dx -> 0 |
Dy Dx |
= 6 |
which means that the slope of the tangent on P (3, 9) of the parabola y = x2 is approximately 6. The general form of the process just described for y = x2 is therefore
| Dy Dx |
= 2x + Dx, and | lim Dx -> 0 |
Dy Dx |
= | lim Dx -> 0 |
(2x + Dx) = 2x |
The derivative, as the general formula for finding the slope of the tangent intersecting a curve at point P = (x, f(x)), is therefore a function that assigns the number mx to a given x by the rule of, for every f(x) = xn, the derivative of x (mp of the tangent at x), f'(x), being nx(n-1). So if f(x) = 2x2 + x4 + 2 then f'(x) = 4x + 4x3. In the case of motion, if x = time and y = position, and the relationship between x and y is that position y = f(x) =..., then velocity is f'(x); to get acceleration, simply replace the values of y by those of velocity, that is, velocity y = f(x) =..., and acceleration would be f'(x) this time.
"Notice that [in the formula of the derivative, Dy/Dx with Dx pushed to 0] Leibniz cannot simply set Dx = 0, for then Dy is also equal to 0. Thus Dy/Dx would be 0/0, which is not defined". (Ibid., p. 118) This is why the slope of the tangent, and so the derivative, is only an approximation. We see again here that the ideal of classical mechanics, absolute precision of measurement and so absolute determination of the future, is logically or mathematically impossible, and that the limitation of the differential calculus itself, that Dx cannot be pushed to 0, implies the uncertainty principle. Since Dx, i.e. time elapsed, and therefore Dy, the indefiniteness of position, cannot be reduced to 0, the velocity calculated thusly can only be approximation, when the line PQ almost coincides with the tangent but never quite yet. If Dx be pushed to 0, then mp, the derivative, i.e. velocity becomes totally indefinite, 0/0. This leads to the uncertainty principle, that if position be determined absolutely accurately, i.e. Dy = 0, then the indefiniteness of momentum (mass x velocity) becomes infinite. Although the actual limit to which Dy and Dx can be pushed is determined, in actual experiments, by the wavelength of the photon, and not by the mathematics itself, that there must be a limit is inherent in the very structure of the "calculus differentialis." That the assumption in classical mechanics based on this calculus, that of absolute determinateness of the derivative, e.g. velocity, then, cannot be correct should have become evident simply on logical and mathematical ground, without and before any experimental confirmations.
The area under the curve, or integration y * x, can represent other factors involved in the phenomenon of the motion of this something: work and energy. In 1675 Leibniz set out to calculate this area under the curve (C), for example between a and b (below)1.
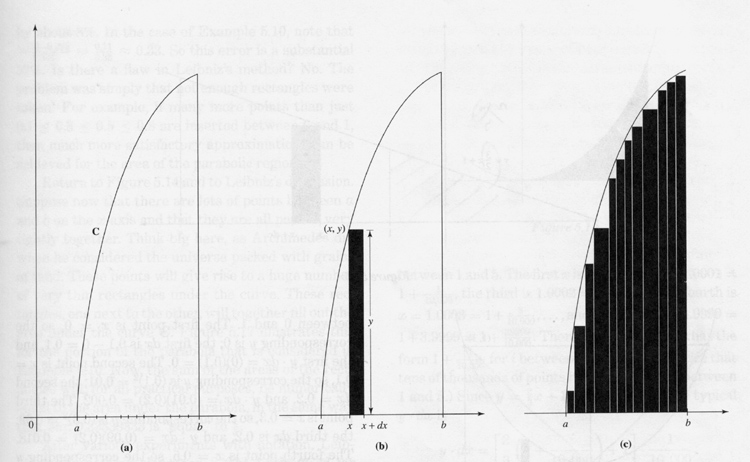
The idea is to cut up the x axis between a and b into many small segments so that for a segment between x and x + dx a rectangle dx * y can be drawn. "Observe that these rectangles, when taken together, fill out -- in an approximate way -- the region under the curve C over the interval from a to b." (Ibid., p. 120) Greater approximation can be achieved by reducing dx, which is to say, by inserting more and more but thinner and thinner rectangles, and the area obtained by adding them all up:
|
In this Naturbild of mechanics, we answer the question of why a, say, resting object starts moving by saying that a force is pulling it in the direction in which it starts moving. Recall that the mechanics took off with Newton's three laws of motion in the Principia:
|
1. That every body perseveres in its state of resting, or of moving uniformly in a right [straight] line, as far as it is not compelled to change that state by an external force impressed upon it.
2. That the change of motion is proportional to the moving force impressed; and is produced in the direction of the right line, in which that force is impressed. 3. That reaction is always contrary and equal to action; or, that the mutual actions of two bodies upon each other are always equal, and directed to contrary parts. (Ibid., p. 180) |
The first law came from Galileo's law of inertia. The second law originally has the formula F = d(mv)/dt, which is basically that F = derivative (d/dt) of momentum p (p = mass x velocity). The "proportionality" in the force's pulling an object to go faster (i.e. increasing its velocity) is therefore that if this object, with mass m, because of this pulling, travels from position a at time t0 to position b at time t1, then the "amount" of force at time t with t0 < or = t < or = t1 pulling this object (m) with now velocity v at this time t is the derivative of the product of mass and velocity at this time t, i.e. that if time be represented by x and the mv by y on the Cartesian coordinates, then force at time t on the object is represented by the slope of the tangent to the curve representing the mv of the object from time t0 to time t 1: F(t) = d/dt(mv(t)), contracted to F = d(mv)/dt. "So the force on the object at any time t is equal to the rate at which the momentum is changing at that time [t]." (Hahn, ibid., p. 493) Later it is written as F = ma since the mass was not known to be capable of varying according to velocity until special relativity.2 "Notice that Newton's first law is a direct consequence of his second law: If the magnitude of a force is zero, then the acceleration it produces in the motion of the body must be zero, and hence its velocity is constant... this is Galileo's law of inertia." (Ibid.)
Note that the third law, that "for every force there is always an equal and opposite force" or that "forces always occur in pair" seems again to point to the symmetry necessitated by Conservation: force always happen in opposite directions in the same amount to cancel itself out in the middle.
In this classical (Newtonian) mechanics, then, the dramatis personnae are mass, its spatial and temporal coordinates, supplemented by inertia and force (which becomes redundant, as discussed).
Mass (body) = density x volume. Mass measures the "how much" of a body, i.e. "how much" of it in a given unit of space times how many units of space this body takes up. "Something" always occupies a certain amount of space and to certain degree of density, which measures, in a word, "how intensely" it occupies space. Mass is therefore a measure, a quantitative representation of the spatiality of a body, how much space it takes up and how intensely it is spatial. So mass is the spatial dimension of an object and motion its temporal dimension, its change of place in space during time elapsed, of which the factors needed for representation are the spatial and temporal coordinates.
To account for this change of place through time "force" is introduced, though redundantly, defined as "an action exerted upon a body, in order to change its state, either at rest, or of uniform motion, in a right [straight] line." (Newton, cited ibid., p. 180) The state is maintained against change by inertia, the internal propensity of the object to resist force, because of and in proportion to its mass (i.e. how intensely and how much it occupies space). Inertia is "power of resisting, by which every body as much as in it lies, perseveres in its state, either of rest, or of uniform motion, in a right [straight] line." (Newton, ibid.) Why this resistance at all? Because "force" is the influence on it to change its original relationship with space by another object, e.g. gravity. But in this way force is just the quantitative measure of the amount of this "influence" on the object for it to dis-place. These "influences" over the total distance of displacement then add up to work, another ("redundant") concept of the classical mechanics. Hence it has a magnitude and direction (and so representable by a vector). Since F = ma, then the direction of influencing/ force is the same as that of acceleration.
We may use the example of gravity to see how work is represented. Galileo noted that the acceleration produced on a body by the force of gravity F during its fall is constant, -g, regardless of the mass of the object. F = -mg = ma. This -mg is precisely the meaning of "weight", the pull by gravity of the body downward toward the center of the earth with the magnitude -mg. Einstein later established the equivalence between acceleration and the force of gravity in this case when formulating general relativity. (-)g is measured to be (approximately) 9.8 meter/second2 around equator of the earth (different than on the north pole, for example, because the earth is not entirely spherical).
g is constant because "[t]he effect of a force on an object is to produce an acceleration proportional to its mass... and the size of the force of gravity on an object is also proportional to its mass. So mass cancels out, and all objects fall at the same rate." (Gribbin, In Search of the Big Bang, p. 76.) The exact quantity of the force of gravity between two bodies is described, "represented", by Newton's universal law of gravitation:
| F = G | mM r2 |
where G is the universal constant of gravitation, r is the distance between the (center of the) two objects in question, and m and M are the respective mass of the two objects.
Now work = force x distance. If a body moves a distance d (from position a to position b) in a straight line due to force f pulling it, then W = f(b - a). Work can therefore be calculated using definite integral.
Let x = distance and y = force, so f(x) with a < or = x < or = b. Assuming f(x) > 0, that is, the magnitude of the force is positive, i.e. pulling the object from a to b rather than reversely from b to a, the case of force having negative magnitude. Procedures: 1. Break up d (from a to b) into n number of very small intervals, each Dx; 2. Assume force to be constant over each interval. 3. Compute the work done on the object over each interval Dx, i.e. a little bit of work: DW1, DW2,... DWi... up to DWn. 4. Add up all these little bits of work. Thus W = DW1 + DW2 + DW2... + DWn =
| n S i = 1 | DWi |
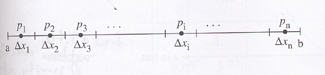 Now, insert a point p in each interval Dx, so that p1 in the first interval Dx1, and p2 in Dx2. (See graph on left.) Then approximately, force over Dx1 = f(p1) and force over Dx2 = f(p2), etc. Since W = fd, DW1 = (approx.) f(p1)Dx1; DW2 = (approx.) f(p2)Dx2;... and DWn = (approx.) f(pn)Dxn. Hence, W = f(p1)Dx1 + f(p2)Dx2... + f(pn)Dxn =
Now, insert a point p in each interval Dx, so that p1 in the first interval Dx1, and p2 in Dx2. (See graph on left.) Then approximately, force over Dx1 = f(p1) and force over Dx2 = f(p2), etc. Since W = fd, DW1 = (approx.) f(p1)Dx1; DW2 = (approx.) f(p2)Dx2;... and DWn = (approx.) f(pn)Dxn. Hence, W = f(p1)Dx1 + f(p2)Dx2... + f(pn)Dxn =
| n S i = 1 | f(pi)Dxi |
Pushing each Dx to smaller and smaller value to make more accurate the approximating of force by a constant and so more tighter the approximation for W, we get:
| W = | lim ||p||->0 | n S i = 1 | f(pi)Dxi |
The assumption is again that y = f(x) or force as a function of distance is continuous. So finally,
|
The property of integration is such that it is the antiderivative of the original function, so (W)' = f(x). To "calculate" (represent) the work of gravity on an object falling from a height of h above the earth's surface:
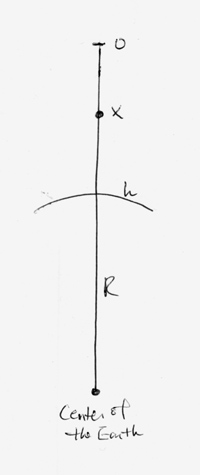 The fall from 0 to h = the distance over which the force of gravity acts.
The fall from 0 to h = the distance over which the force of gravity acts.
Using Newton's equation (1 dimensional quantitative representation) for universal gravitation, we see that the force of gravity at point x on the object is
| G | mM (R + h - x)2 |
where M = mass of the earth, m = mass of the falling object, and (R + h - x) = the distance between earth's center and the object. Work of gravity on the object from 0 to h is then,
|
In this "representation", the phenomenon (the work of gravity pulling the falling object) is dissected along the axes of the magnitude of force and the distance over which it acts and then reconstituted through the relationship between the two (in this case, multiplication, or integration). Or rather, "work" is simply a redundant concept in the sense of not having independent status, since it is merely the artificial composite of two other concepts, force and distance, with force itself an artificial composite (this time formed of differentiation) of momentum and time. That is, they are both merely kinematic, i.e. space-time descriptions, without causal connotations. That Newton was well aware, or rather intended, that the "proportionality" of the "alteration of the quantity of motion" to "the motive force impressed" specified in his second law or the inverse square law of universal gravity be only a quantitative representation (descriptive) without causal meaning, without explaining the reason for anything, was the meaning of his words: "But hitherto I have not been able to discover the cause of those properties of gravity from phenomena, and I frame no hypothesis (hypotheses non fingo)." (Cited by Dugas, History of Mechanics, p. 200) Or "I likewise... use the words Attraction, Impulse or Propensity of any sort towards a center, promiscuously and indifferently, one for another; considering those forces not Physically but Mathematically --" (Ibid., p. 203) The inability to discover the cause of force led d'Alembert to declare that "mechanics is a science of effects and has nothing to do with causes. The 'force of motion' has no meaning apart from the effect that the moving body produces." (Thomas Hankins' introduction to d'Alembert's Traité de Dynamique, xxi) D'Alembert consequently banished force from his mechanics as useless. Laplace likewise spoke in the same spirit in Mécanique céleste: "The mechanism of that remarkable agency, force, by which a body is moved from one place to another, is and always will be unknown. It is only possible to determine the laws which govern its behaviour [i.e. kinematics, space-time description]." (Cited by Dugas, ibid., p. 354) This is the deficiency of classical mechanics. Relativity and quantum mechanics, the new physics, have been able to overcome this deficiency. We have already seen that Bohm has noted the irreducibility of concepts like energy and momentum in quantum mechanics, providing the fundamental units of causality. General relativity has explained gravity as caused by the warping of space-time continuum by the mass of the bodies in it; quantum field theory is able to explain the reason for (just about) all the four forces, at least preliminarily (before the total unified theory), the reason as to why they are the way they are, for example in terms of the spin of the particles in the exchange process in terms of which it sees all subatomic interactions (forces): "The exchange of a spin 0 particle produces an attractive force, of a spin 1 particle a repulsive force, and of a spin 2 particle an attractive force, realized in the hadronic strong interaction, the electromagnetic interaction, and the gravitational interaction, respectively." (A. Zee, Quantum Field Theory in a Nutshell, 2003, p. 35)
Before we turn to energy, we must go over the fundamental theorem of calculus presented by Leibniz, in 1693, in Acta Eruditorum. (Hahn, ibid. p. 126) The theorem is to establish a fundamental relationship between the slope of the tangent and the area under the curve.
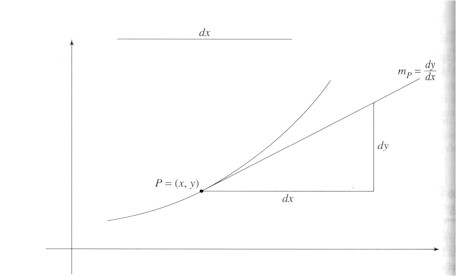 In the figure on the left, mp, slope of the tangent = dy/dx. dy = mp * dx. dx is designated by Leibniz as the differential of x, dy (i.e. mp * dx) the differential of y, and the triangle formed of dx, dy and mp the characteristic triangle. The choice of dx is arbitrary. For a parabola y = x2, then, mp = 2x and dy = 2x * dx, and for a curve y = x3, mp = 3x2 and dy = 3x2 * dx.
In the figure on the left, mp, slope of the tangent = dy/dx. dy = mp * dx. dx is designated by Leibniz as the differential of x, dy (i.e. mp * dx) the differential of y, and the triangle formed of dx, dy and mp the characteristic triangle. The choice of dx is arbitrary. For a parabola y = x2, then, mp = 2x and dy = 2x * dx, and for a curve y = x3, mp = 3x2 and dy = 3x2 * dx.
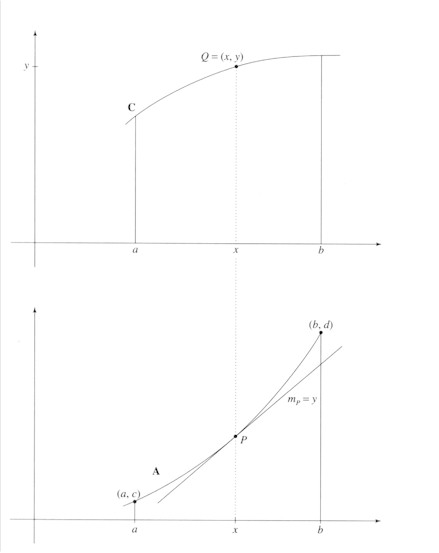
The fundamental relationship between the slope of the tangent mp (differentiation) and the area under the curve (integration) is possible because for a curve A there can always be a curve C (figure 2) such that mp or dy/dx of the tangent for curve A is equal to y of Q (x, y) on curve C, and the area dx * y = dy (figure 3). Then the area under the curve is:
|
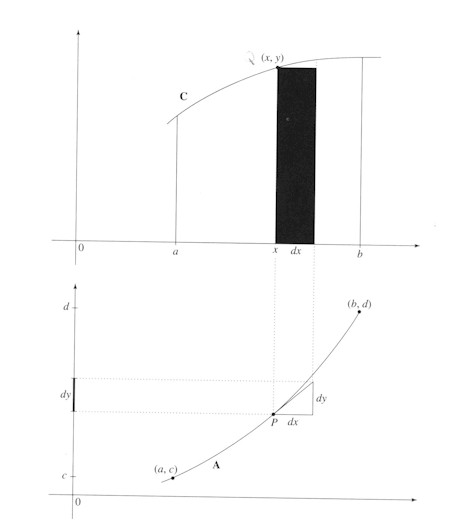
i.e. the sum of all tiny rectangles y * dx = the sum of all dys of the corresponding characteristic triangle dxdy between c and d (figure 4).
|
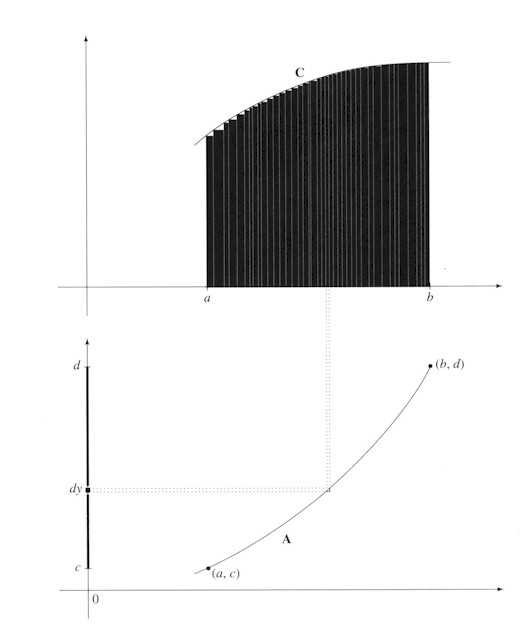
Figure 4
For example, let curve C = y = x2 and curve A = y = Ax3. The mp of the tangent for y = Ax3 at point P on it is the differential d/dx(Ax3) = 3Ax2. If A = 1/3, then mp = x2 = curve C's y = x2. "Therefore, the graph of y = 1/3x3 [Curve A] has the property that the slope of the tangent mp at x is equal to the y-coordinate of the point on C at x." (Ibid., p. 128) If x = 0, then y of A = 0; if x = 1, then y of A = 1/3, and the area under the curve y = x2 between 0 < or = x < or = 1 is d - c = 1/3 - 0 = 1/3.
We now turn to energy. Of the 4 kinds of energy enumerated, kinetic energy (of a moving body with mass m and velocity v) is "represented" as 1/2mv2. So an automobile of mass 900 kg. moving at 25m/sec has the kinetic energy of 1/2(900)(25)2 = 450 * 625 = 281,250 kg-(m/sec)2 (Hahn, ibid., p. 482). The relationship between work and kinetic energy can be demonstrated calculusically.
For an object, again, moving from a at time t0 to b at time t1, has position x(t), velocity x'(t), and acceleration x"(t). This is one Cartesian coordinate, x = t and y = position. Let force = f(x), i.e. function of position. By Newton's second law f(x(t)) = ma(t) = mx"(t). This is another Cartesian coordinate, where y = force and x = time, based on still another coordinate, where x = time and y = momentum mv, and F = d/dt(mv) at time t. Now
|
The sum of forces (each over an infinitesimal distance Dx) over distance b - a is reformulated as the sum of forces (each as function to position at time t) over time t1 - t0. That x'(t)dt = dx means velocity times time is equal to distance travelled within this time, as can be seen in (distance travelled: b - a)/(time elapsed: t1 - t0) * (time elapsed: t1 - t0).
If we take the derivative of the kinetic energy at time t:
| d dt | ( | 1 2 | mv(t)2) = mv(t) | dv dt | (t) = f(x(t))x'(t) |
"So the kinetic energy function 1/2mv(t)2 is an anti-derivative [integration] of f(x(t))x'(t) [i.e. the work done at the instant t]." (Ibid., p. 483) Therefore by the fundamental theorem of calculus:
| W = |
ó õ |
t1 t0 | f(x(t))x'(t)dt = | 1 2 | mv(t1)2 - | 1 2 | mv(t0)2 |
So the work done on the object by force as it moves from a to b is equal to the kinetic energy of the object at b minus the kinetic energy of the object at a. Hence, work is the change that force effects in the kinetic energy of the object. "If the object starts from rest, then v(t0) = 0 and 1/2mv(t0)2 = 0. In this case, W = 1/2mv(t1)2. So the work done on the object [by force causing it to move] is equal to the kinetic energy that the object picks up during its motion [due to force]." (Ibid.) Work is the sum of all forces (each over an infinitesimal distance Dx) over the total distance, and is the same as the kinetic energy of the object at the end of the travel. Thus force transfers onto the object a certain amount of energy called work, which is then the energy with which the object can do an equal amount of work. This can be seen from the derivation of the kinetic energy function itself. For W = fd = mad; v = at (acceleration times time), so that t = v/a. In Galileo's experiment it has already been demonstrated that d = 1/2at2, where d = distance covered by the moving object. So d = 1/2a(v/a)2 = (1/2)(v2/a). W = 1/2(mav2/a) = mad = ma(1/2(v2/a)) = 1/2(mav2/a) = 1/2mv2. We have shown in another way that work = kinetic energy. (C.f. Asimov, Understanding Physics, p. 95) The term energy was first proposed by Thomas Young in 1807 to designate the "work-store", i.e. the amount of energy transferred during work onto an object which can be transformed again into the equal amount of work. Kinetic energy was proposed by Lord Kelvin in 1856.
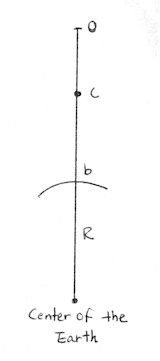 Now the potential energy. Consider an object at rest at 0 starting to fall toward the earth's center because of the force of gravity, until it hits the surface at b (figure at left). The kinetic energy of the object at an arbitrary midpoint c is:
Now the potential energy. Consider an object at rest at 0 starting to fall toward the earth's center because of the force of gravity, until it hits the surface at b (figure at left). The kinetic energy of the object at an arbitrary midpoint c is:
|
The object has the potential of gaining additional kinetic energy between point c and b:
|
This is a case of gravitational potential energy, PEg = mgy, where g is Galileo's accelerational constant and y the distance to be travelled; i.e. W = mad = 1/2mv2 at the end of distance. The kinetic + potential energy = the total mechanical energy of the object (i.e. due to its motion) which addition is always the same, i.e. the kinetic energy of the object at the end of its travel: the conservation of mechanical energy:
| 1 2 | m(vc)2 + ( |
1 2 | m(vb)2 - | 1 2 | m(vc)2) = | 1 2 | m(vb)2 |
But remember that the "true" conservation of energy applies only at the total level, i.e. mechanical energy + rest/ internal energy (E = mc2) of the object.
Footnotes:
1. Based on Alexander Hahn, Basic Calculus, p. 121 - 3.
2. C.f. Peter Beckmann, A History of p, 1971, St. Martin's Press, N.Y., p. 135: "Newton's laws of motion are not contradicted by Einstein's theory of special relativity. Newton never made the statement that Force = mass x acceleration. His second law says: F = d(mv)/dt and Newton was far more cautious a man to take the m out of the bracket. When mass, in Einstein's interpretation, became a function of velocity, not an iota in Newton's laws needed to be changed." What this means is that if force is seen as a function of time F(t), and the mass of the object as changing, so that m = m(t), then F(t) = d/dt(m(t)v(t)). "In the case where m = m(t) is a constant, this says that F(t) = m(d/dt)(v(t)) = ma(t). Therefore, F(t) = d/dt(m(t)v(t)) is Newton's second law formulated in a way that allows the mass of the object to vary" (Hahn, ibid., p. 494).
| ACADEMY | previous section | Table of Content | next section | GALLERY |